GMM Stevie: Exploring Innovations in Music and Technology

GMM Stevie Wynne Levine is a key figure behind the popular YouTube series Good Mythical Morning (GMM). Since joining the team in 2013, she has played an important role as an executive producer and Chief Creative Officer for Mythical Entertainment.

Her creativity and leadership have helped shape GMM into one of the most-watched daily shows on the internet.

Audiences not only enjoy the entertaining content of GMM, but they also appreciate the unique voice of Stevie. She brings a fresh perspective as the narrator in many episodes and connects with viewers in a personal way. Her influence extends beyond just GMM, as she continues to innovate within various shows and platforms under the Mythical brand.

Fans of GMM often wonder about Stevie’s journey and contributions. Learning more about her role reveals how her work enhances the series’ comedic style and audience engagement. Exploring Stevie’s background offers insight into the successful formula that makes Good Mythical Morning a standout series.

Key Takeaways

• Stevie Wynne Levine is a central figure in the success of Good Mythical Morning.
• Her contributions include being a narrator and executive producer for the show.
• Understanding her role highlights the creative processes behind popular online content.

The Fundamentals of Gaussian Mixture Models

Gaussian Mixture Models (GMMs) provide a flexible method for representing complex data distributions. They combine multiple Gaussian distributions to model data that may have various underlying patterns. This section covers the core definition and the mathematical principles that form the basis of GMMs.

Definition and Overview

A Gaussian Mixture Model is a statistical model that represents a distribution as a combination of several Gaussian distributions. Each component of the model is defined by its own mean and variance.

GMMs are particularly useful for clustering, where data points are assigned to different groups based on their probabilities. The model assumes that data points originate from one of several distributions but does not specify which point belongs to which distribution. This property makes GMMs powerful for unsupervised learning tasks.

Mathematical Concepts Underlying GMMs

The foundation of GMMs lies in probability and statistics. Each Gaussian component can be described by the formula:

[ f(x) = \frac{1}{\sqrt{2\pi\sigma^2}} e^{-\frac{(x-\mu)^2}{2\sigma^2}} ]

where:

• ( \mu ) is the mean,
• ( \sigma^2 ) is the variance.

A GMM consists of multiple such equations, weighted by a mixing coefficient for each component. The mixing coefficients represent the probability of a data point belonging to a specific Gaussian distribution.

To estimate the parameters (means, variances, and weights), GMMs typically use the Expectation-Maximization (EM) algorithm. This iterative method alternates between estimating the probability of each data point belonging to a distribution and refining the parameters based on these estimates.

In summary, GMMs offer a robust framework for modeling and understanding complex data distributions through the combination of simple Gaussian functions.

Application of GMM in Machine Learning

Gaussian Mixture Models (GMM) are powerful tools in machine learning, particularly for tasks involving probabilistic modeling. Their flexibility enables them to be useful across various domains, including pattern recognition, speech and image processing, and bioinformatics.

Pattern Recognition

GMMs play a vital role in pattern recognition tasks. They help identify complex patterns within data by modeling the distribution of data points.

• Data Clustering: GMMs can effectively cluster high-dimensional data. They provide a probabilistic approach to determine which cluster a data point belongs to, based on its likelihood.
• Subtle Variations: This model captures subtle variations between clusters that other methods, like K-means, might overlook.

This makes GMMs suitable for applications in fields like computer vision, where distinguishing between different shapes or images is crucial.

Speech and Image Processing

In speech and image processing, GMMs have a wide range of applications. They assist in the analysis and generation of data.

• Speech Recognition: GMMs model the acoustic features of spoken words. By estimating the distribution of these features, they help improve the accuracy of recognizing spoken language.
• Image Segmentation: In image processing, GMMs are used for segmenting images into different regions. They help classify pixels based on color intensity and spatial relationships.

This application enhances the ability to process and analyze large amounts of visual and auditory data effectively.

Bioinformatics

GMMs are also valuable in bioinformatics, particularly in analyzing biological data.

• Gene Expression Analysis: GMMs can classify different patterns in gene expression levels. By modeling the distributions of gene expressions, they help researchers identify significant biological markers.
• Protein Structure Prediction: In understanding protein structures, GMMs assist in classifying conformations based on specific statistical properties.

Their ability to manage complexity makes GMMs an important tool in these areas of biological research and analysis.

Stevie, the GMM-Based Programming Language

Stevie is a programming language inspired by the themes and formats of Good Mythical Morning (GMM). It focuses on ease of use and creative expression, making it accessible for beginners and engaging for experienced programmers. The following subsections provide insights into its syntax, compiler architecture, and practical code examples.

Stevie Language Syntax

Stevie’s syntax is designed to be intuitive and straightforward. It uses familiar programming constructs to lower the learning curve for new users. Key components include:

• Variable Declaration: Variables can be declared using simple keywords. For example: let magicNumber = 42;
• Function Definition: Functions are defined with a clear syntax: function greet(name) { return "Hello, " + name; }
• Control Structures: It supports common control structures like loops and conditionals. For instance: if (magicNumber > 0) { print("Positive!"); }

This simplicity allows users to focus on creativity rather than complex rules.

Stevie Compiler Architecture

The architecture of the Stevie compiler is modular and efficient. It consists of several key components:

• Parser: The parser interprets the source code and builds an Abstract Syntax Tree (AST). This structure represents the code’s logical flow.
• Semantic Analyzer: This component checks for semantic errors, ensuring that the code adheres to the rules of the Stevie language.
• Code Generator: The code generator translates the AST into executable code optimized for performance.
• Error Handling: The compiler provides clear error messages to guide users in debugging their code.

This architecture allows Stevie to be both powerful and user-friendly, making coding a more enjoyable experience.

Code Examples in Stevie

Here are some code examples that showcase Stevie’s features:

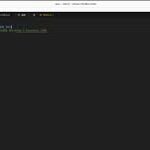
1. Basic Output: print("Welcome to Stevie!");
2. Simple Loop: for (let i = 0; i < 5; i++) { print("Count is: " + i); }
3. Conditional Execution: let score = 85; if (score >= 60) { print("You passed!"); } else { print("Try again."); }

These examples illustrate how simple yet effective Stevie can be in creating engaging programs. The language encourages experimentation, aligning well with the playful spirit of GMM.